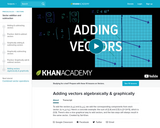
To add the vectors (x₁,y₁) and (x₂,y₂), we add the corresponding components from each vector: (x₁+x₂,y₁+y₂). Here's a concrete example: the sum of (2,4) and (1,5) is (2+1,4+5), which is (3,9). There's also a nice graphical way to add vectors, and the two ways will always result in the same vector.​​

Describe a bivariate relationship's linearity, strength, and direction. In other words, plotting things that take two variables into consideration and trying to see whether there's a pattern with how they relate.

The most common way to calculate the correlation coefficient (r) is by using technology, but using the formula can help us understand how r measures the direction and strength of the linear association between two quantitative variables.

This is a brief conditional probability examplediscussing probabilities like P(A | B) using breakfast and lunch as examples.

The most common way to calculate the correlation coefficient (r) is by using technology, but using the formula can help us understand how r measures the direction and strength of the linear association between two quantitative variables.

This video talka about what is easily one of the most fundamental and profound concepts in statistics and maybe in all of mathematics. And that's the central limit theorem.

Overview of Communism and Marxist-Leninist states. For extra coverage of the Cold War outside the scope of the AP course, click here. Created by Sal Khan.

Understanding why correlation does not imply causality (even though many in the press and some researchers often imply otherwise).

Sal discusses the conditions of matrix dimensions for which addition or multiplication are defined. Created by Sal Khan.

Sociology often looks at different age cohorts. A cohort is simply a group of people, but here we're looking specifically at different age groups or generations, because these people all lived through the same certain events through a certain time that affected their lives similarly.

This video defines the differences between discrete and continuous random variables, then works through examples of each.

Discrimination can be defined in two ways: individual and institutional. Individual discrimination refers to the prejudiced behavior of one person, while institutional discrimination refers to the way an organization's rules or policies disadvantage certain groups. Although they are distinct, these two forms of discrimination can be interconnected. Individual discrimination can be reinforced by institutional policies, and vice versa, which leads to a larger, systemic issue. (. Created by James Howick.

Where we live in society plays a huge role in the environmental benefits and risks that we're exposed to.